2. Burrows Delta verstehen
2.1. Überblick zum Forschungsstand
Burrows Delta ist einer der erfolgreichsten Algorithmen der Computational Stylistics (Burrows 2002). In einer ganzen Reihe von Studien wurde seine Brauchbarkeit nachgewiesen (z. B. Hoover 2004, Rybicki / Eder 2011). Im ersten Schritt bei der Berechnung von Delta werden in einer nach Häufigkeit sortierten Token-Dokument-Matrix alle Werte normalisiert, indem ihre relative Häufigkeit im Dokument berechnet wird, um Textlängenunterschiede auszugleichen. Im zweiten Schritt werden alle Werte durch eine z-Transformation standardisiert:
wobei f i( D) die relative Häufigkeit des Wortes i in einem Dokument, μ i der Mittelwert über die relativen Häufigkeiten des Wortes i in allen Dokumenten ist und σ i die Standardabweichung. Durch diese Standardisierung tragen alle Worte in gleichem Maße zum Differenzprofil, das im dritten Schritt berechnet wird, bei. In einem dritten Schritt werden die Abstände aller Texte voneinander berechnet: Für jedes Wort wird die Differenz zwischen dem z-Score für das Wort in dem einen Text und dem anderen Text ermittelt. Die Absolutbeträge der Differenzen werden für alle ausgewählten Wörter aufaddiert:
m steht für die Anzahl der häufigsten Wörter (MFW - most frequent words), die für die Untersuchung herangezogen werden. Diese Summe ergibt den Abstand zwischen zwei Texten; je kleiner der Wert ist, desto ähnlicher – so die gängige Interpretation – sind sich die Texte stilistisch, und desto höher ist die Wahrscheinlichkeit, dass sie vom selben Autor verfasst wurden.
Trotz seiner Einfachheit und seiner praktischen Nützlichkeit mangelt es bislang allerdings an einer Erklärung für die Funktionsweise des Algorithmus. Argamon (2008) zeigt, dass der dritte Schritt in Burrows Delta sich als Berechnung des Manhattan-Abstands zwischen zwei Punkten in einem mehrdimensionalen Raum verstehen lässt, wobei in jeder Dimension die Häufigkeit eines bestimmten Wortes eingetragen ist. Er schlägt vor, stattdessen den Euklidischen Abstand, also die Länge der direkten Linie zwischen den Punkten, zu nehmen, weil dieser „possibly more natural“ (Argamon 2008: 134) sei und zudem eine wahrscheinlichkeitstheoretische Interpretation der standardisierten z-Werte erlaubt. Bei einer empirischen Prüfung zeigte sich, dass keiner der Vorschläge eine Verbesserung bringt (Jannidis et al. 2015).
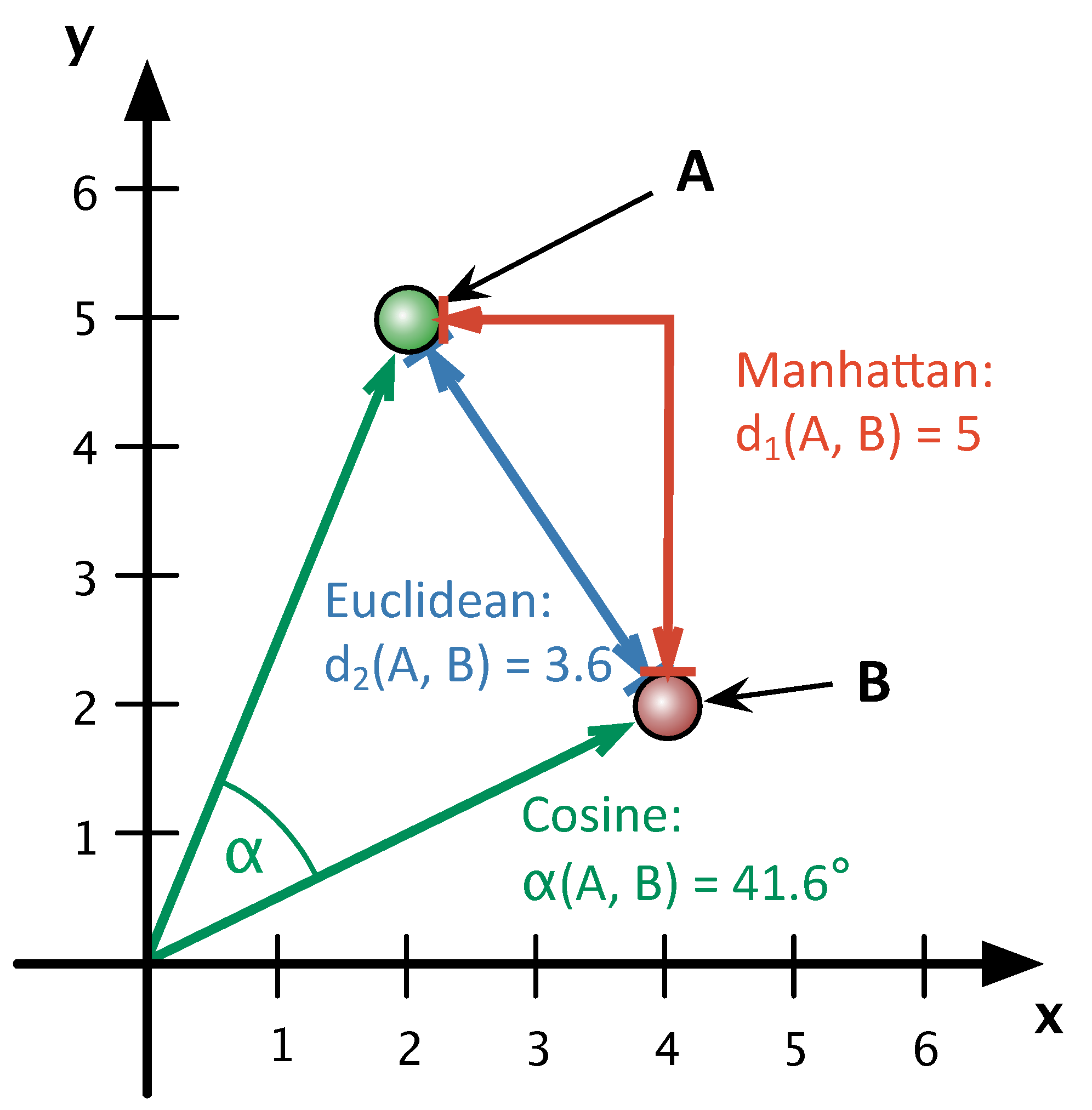
Abb. 1: Darstellung des Abstands zwischen zwei Texten, die nur aus zwei Worten bestehen. Burrows Delta verwendet die Manhattan-Distanz. Argamons Vorschlag, die Euklidische Distanz zu verwenden, sein Quadratic-Delta, brachte eine Verschlechterung der Clustering Ergebnisse, während der Vorschlag von Smith und Aldrige, den Cosinus-Abstand bzw. Winkel zwischen den Vektoren zu verwenden, eine deutliche Verbesserung erbrachte.
Smith und Aldrige (2011) schlagen vor, wie im Information Retrieval üblich (Baeza-Yates / Ribeiro-Neto 1999: 27), den Cosinus des Winkels zwischen den Dokumentenverktoren zu verwenden. Die Cosinus-Variante von Delta übertrifft Burrows Delta fast immer an Leistungsfähigkeit und weist, im Gegensatz zu den anderen Varianten, auch bei der Verwendung sehr vieler MFWs keine Verschlechterung auf (Jannidis et. al. 2015). Es stellt sich die Frage, warum Delta Cos besser ist als Delta Bur und ob auf diese Weise erklärt werden kann, warum Delta Bur so überraschend leistungsfähig ist.
Entscheidend für unsere weitere Analyse war die Erkenntnis, dass man die Verwendung des Cosinus-Abstands als eine Vektor-Normalisierung verstehen kann, da für die Berechnung des Winkels – anders als bei Manhattan- und Euklidischem Abstand – die Länge der Vektoren keine Rolle spielt (vgl. Abb. 1). Experimente haben gezeigt, dass eine explizite Vektor-Normalisierung auch die Ergebnisse der anderen Deltamaße erheblich verbessert und Leistungsunterschiede zwischen den Delta-Varianten weitgehend neutralisiert (Evert et al. 2015).
Daraus wurden zwei Hypothesen abgeleitet:
- (H1) Verantwortlich für die Leistungsunterschiede sind vor allem einzelne Extremwerte („Ausreißer“), d. h. besonders große (positive oder negative) z-Werte, die nicht für Autoren, sondern nur für einzelne Texte spezifisch sind. Da das Euklidische Abstandsmaß besonders stark von solchen Ausreißern beeinflusst wird, stellen sie eine nahe liegende Erklärung für das schlechte Abschneiden von Argamons „Quadratic Delta“ Delta Q. Der positive Effekt der Vektor-Normalisierung wäre dann so zu deuten, dass durch die Vereinheitlichung der Vektorlängen der Betrag der z-Werte von textspezifischen Ausreißern deutlich reduziert wird (Ausreißer-Hypothese).
- (H2) Das charakteristische stilistische Profil eines Autors findet sich eher in der qualitativen Kombination bestimmter Wortpräferenzen, also im grundsätzlichen Muster von über- bzw. unterdurchschnittlich häufigem Gebrauch der Wörter, als in der Amplitude dieser Abweichungen. Ein Textabstandsmaß ist vor allem dann erfolgreich, wenn es strukturelle Unterschiede der Vorlieben eines Autors erfasst, ohne sich davon beeinflussen zu lassen, wie stark das Autorenprofil in einem bestimmten Text ausgeprägt ist (Schlüsselprofil-Hypothese). Diese Hypothese erklärt unmittelbar, warum die Vektor-Normalisierung zu einer so eindrucksvollen Verbesserung führt: durch sie wird die Amplitude des Autorenprofils in verschiedenen Texten vereinheitlicht.
2.2. Neue Erkenntnisse
2.2.1. Korpora
Für die hier präsentierten Untersuchungen verwenden wir drei vergleichbar aufgebaute Korpora in Deutsch, Englisch und Französisch. Jedes Korpus enthält je 3 Romane von 25 verschiedenen Autoren, insgesamt also jeweils 75 Texte. Die deutschen Romane aus dem 19. und dem Anfang des 20. Jahrhunderts stammen aus der Digitalen Bibliothek von TextGrid. Die englischen Texte aus den Jahren 1838 bis 1921 kommen von Project Gutenberg und die französischen Romane von Ebooks libres et gratuits umfassen den Zeitraum von 1827 bis 1934. Im folgenden Abschnitt stellen wir aus Platzgründen nur unsere Beobachtungen für das deutsche Romankorpus vor. Die Ergebnisse mit Texten in den beiden anderen Sprachen bestätigen – mit kleinen Abweichungen – unseren Befund.
2.2.2. Experimente
Um die Rolle von Ausreißern und damit die Plausibilität von H1 näher zu untersuchen, ergänzen wir Delta Bur und Delta Q um weitere Delta-Varianten, die auf dem allgemeinen Minkowski-Abstand basieren:
für p ≥ 1.
Wir bezeichnen diese Abstandsmaße allgemein als L p-Delta. Der Spezialfall p = 1 entspricht dem Manhattan-Abstand (also L 1-Delta = Delta Bur), der Spezialfall p = 2 dem Euklidischen Abstand (also L 2-Delta = Delta Q). Je größer p gewählt wird, desto stärker wird L p-Delta von einzelnen Ausreißerwerten beeinflusst.
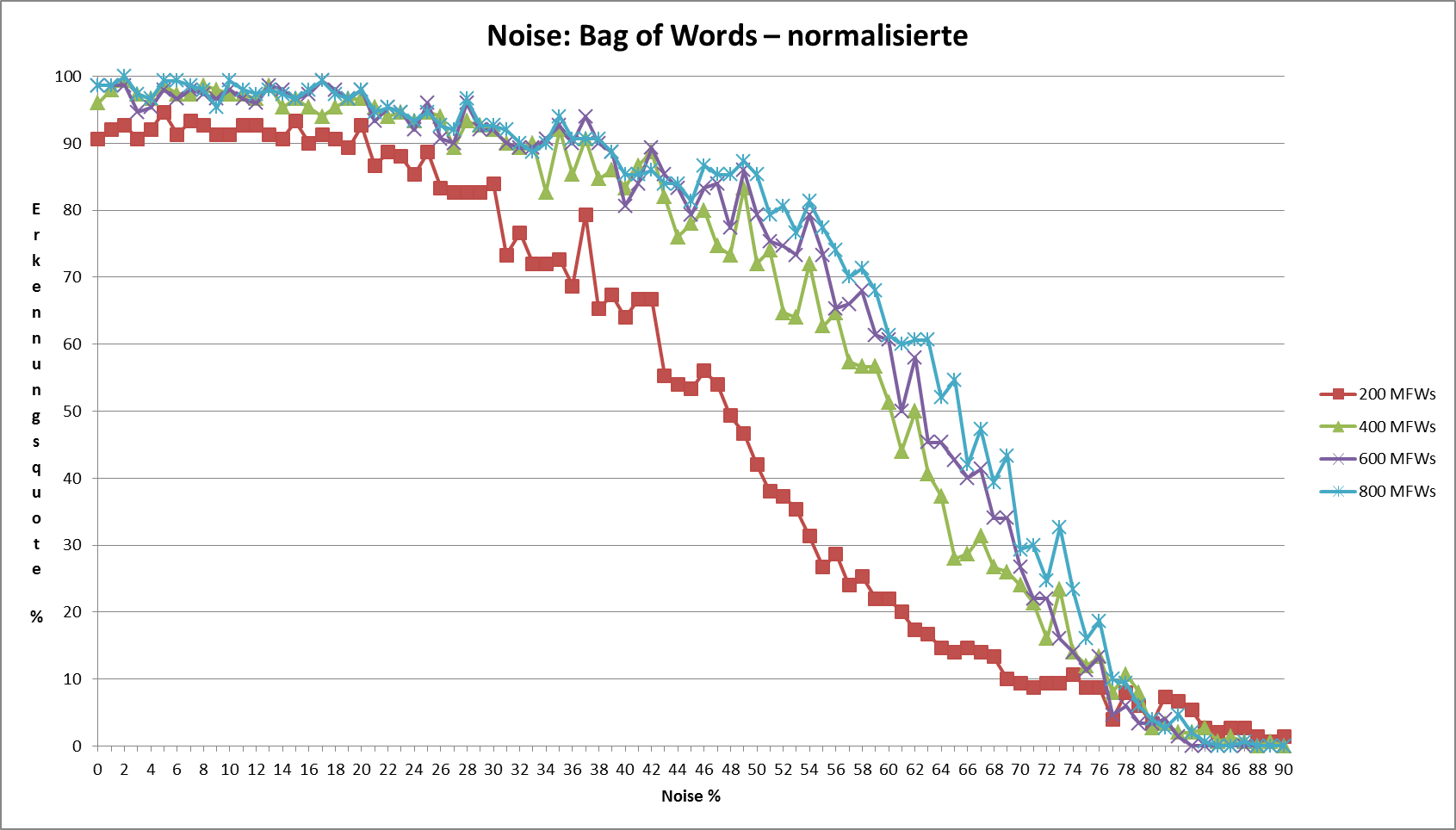
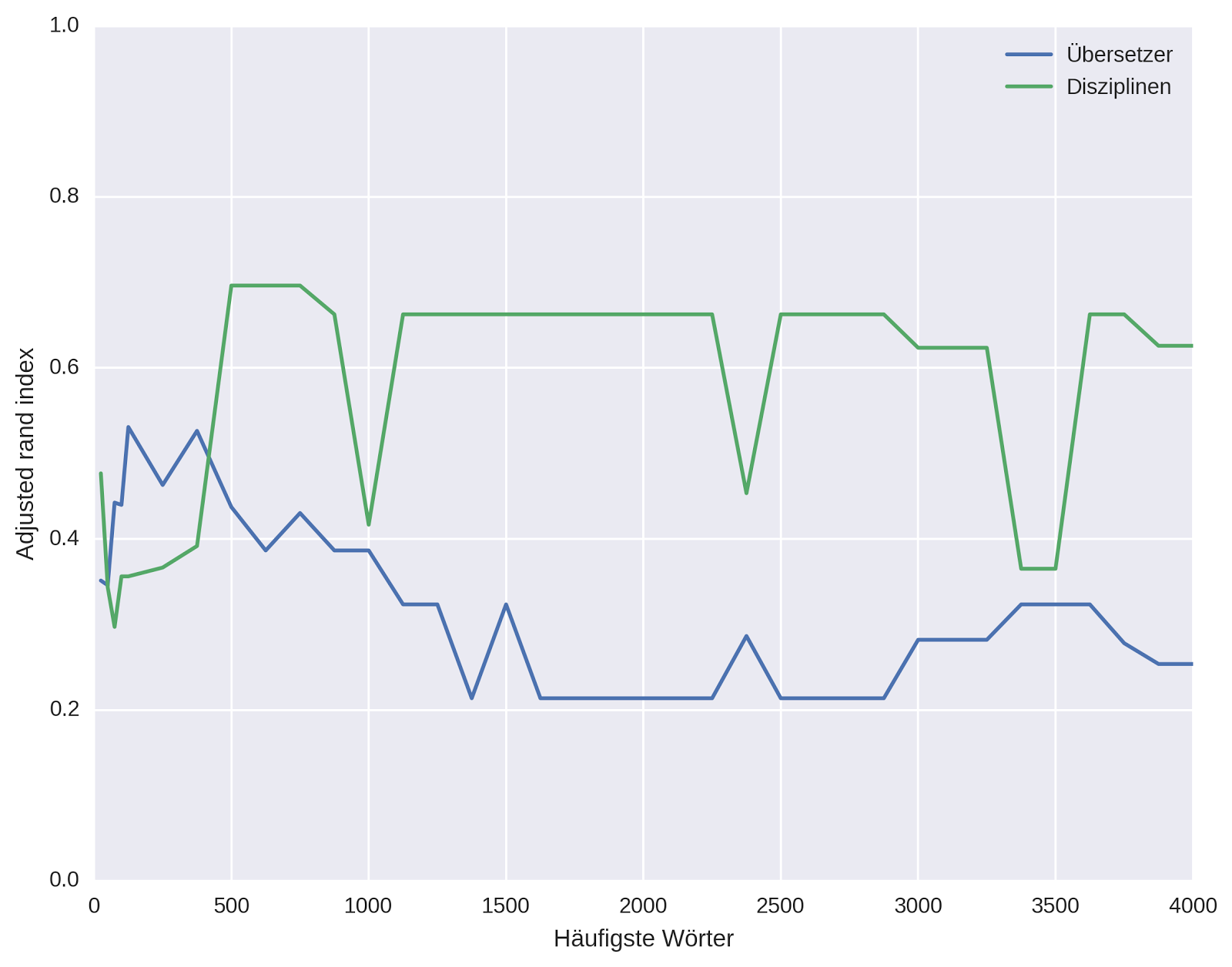
Abbildung 2 vergleicht vier unterschiedliche L p-Abstandsmaße (für ) mit Delta Cos. Wir übernehmen dabei den methodologischen Ansatz von Evert et al. (2015): die 75 Texte werden auf Basis der jeweiligen Delta-Abstände automatisch in 25 Cluster gruppiert; anschließend wird die Güte der Autorenschaftszuschreibung mit Hilfe des adjusted Rand index (ARI) bestimmt. Ein ARI-Wert von 100% entspricht dabei einer perfekten Erkennung der Autoren, ein Wert von 0% einem rein zufälligen Clustering. Offensichtlich nimmt die Leistung von L p-Delta mit zunehmendem p ab; zudem lässt die Robustheit der Maße gegenüber der Anzahl von MFW erheblich nach.
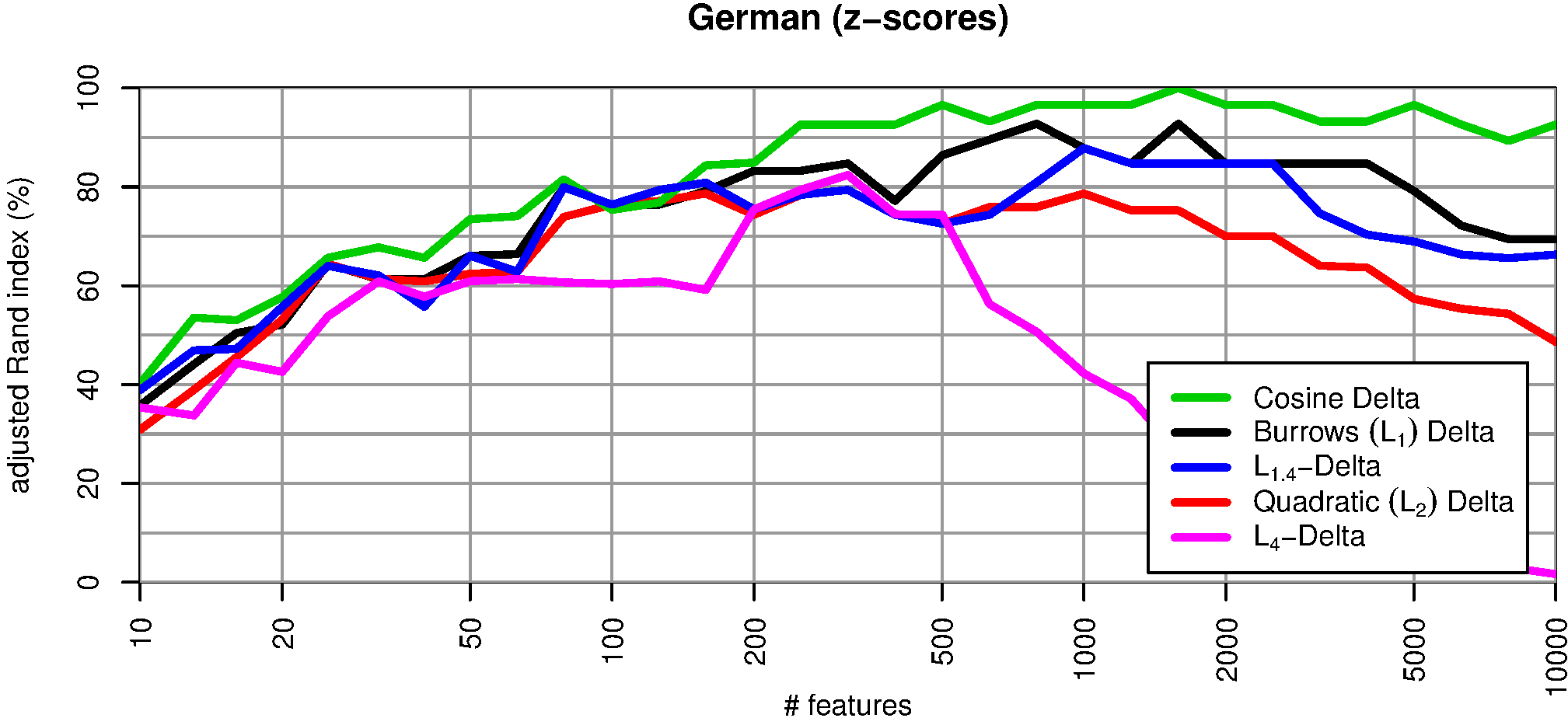
Abb. 2: Clustering-Qualität verschiedener Delta-Maße in Abhängigkeit von der Anzahl von MFW, die als Merkmale verwendet werden. Wie bereits von Janndis et al. (2015) und Evert et al. (2015) festgestellt wurde, liefert Delta Bur (L 1) durchgänig bessere Ergebnisse als Argamons Delta Q (L 2). Delta Q erweist sich als besonders anfällig gegenüber einer zu großen Anzahl von MFW. Delta Cos ist in dieser Hinsicht robuster als alle anderen Delta-Varianten und erreicht über einen weiten Wertebereich eine nahezu perfekte Autorenschaftszuschreibung (ARI > 90%).
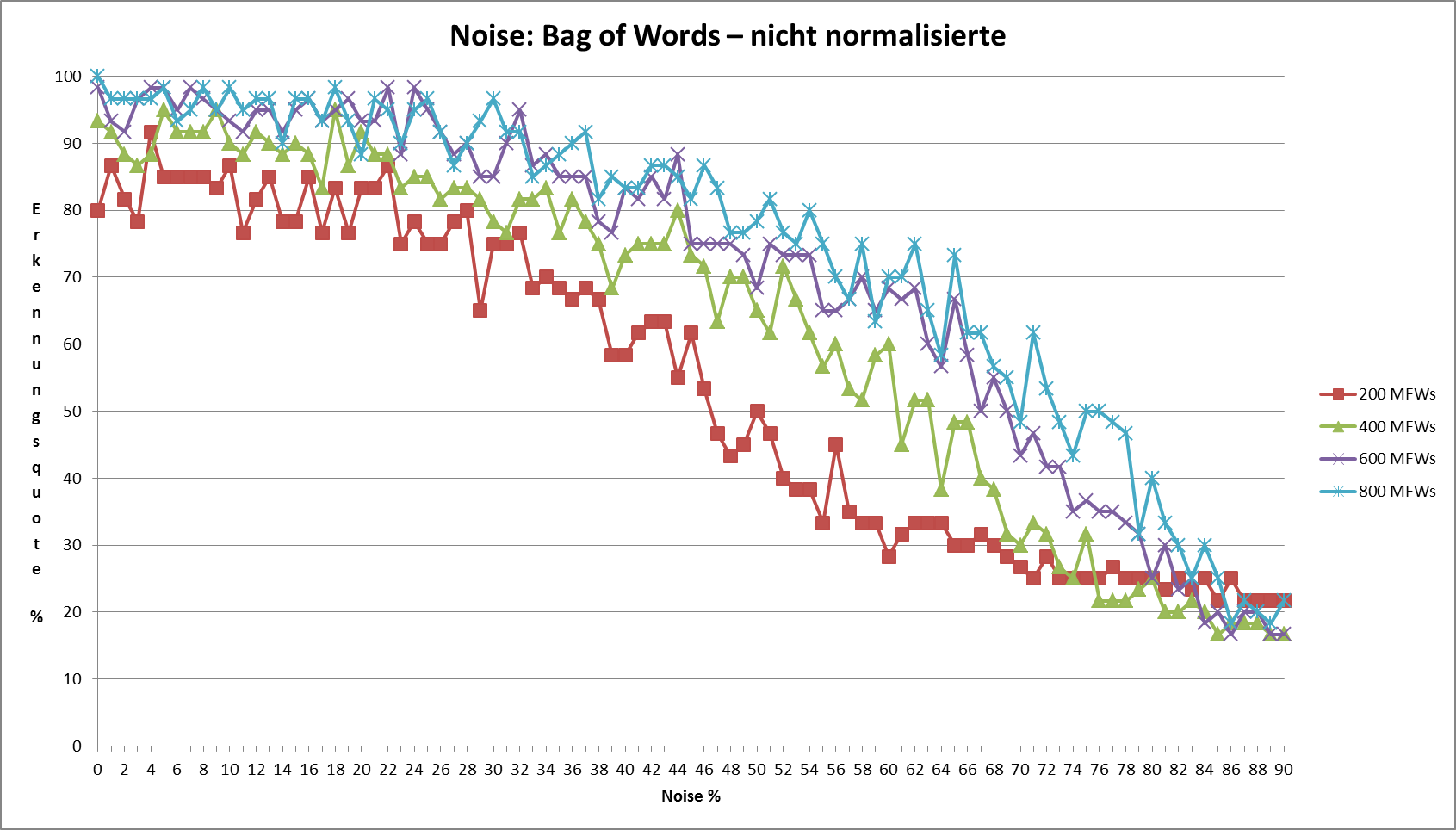
Eine Vektor-Normalisierung verbessert die Qualität aller Delta-Maße erheblich (vgl. Abb. 3). Argamons Delta Q ist in diesem Fall identisch zu Delta Cos: die rote Kurve wird von der grünen vollständig überdeckt. Aber auch andere Delta-Maße (Delta Bur, L 1.4-Delta) erzielen praktisch dieselbe Qualität wie Delta Cos. Einzig das für Ausreißer besonders anfällige L 4-Delta fällt noch deutlich gegenüber den anderen Maßen ab. Diese Ergebnisse scheinen zunächst H1 zu bestätigen.
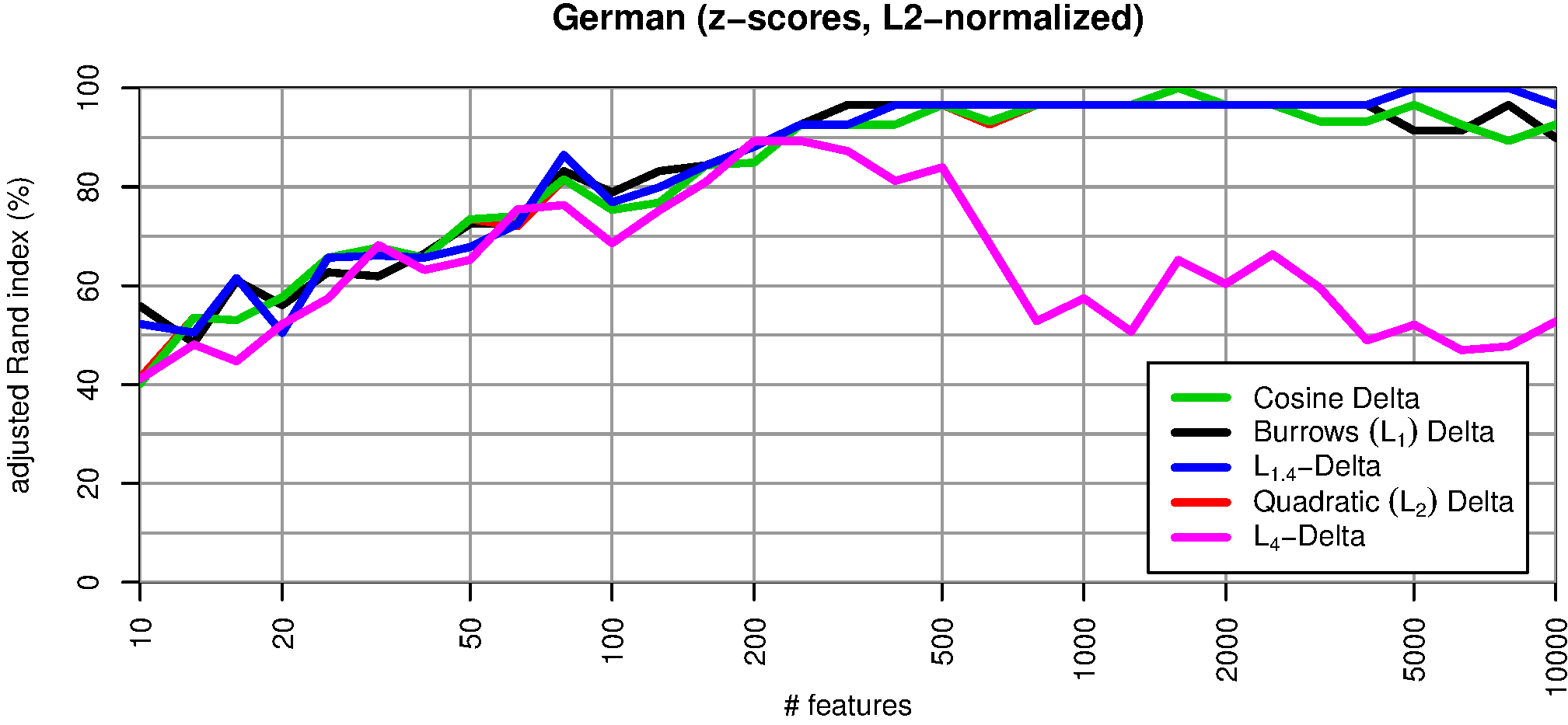
Abb. 3: Clustering-Qualität verschiedener Delta-Maße mit Längen-Normalisierung der Vektoren. In diesem Experiment wurde die euklidische Länge der Vektoren vor Anwendung der Abstandsmaße auf den Standardwert 1 vereinheitlicht.
Ein anderer Ansatz zur Abmilderung von Ausreißern besteht darin, besonders extreme z-Werte „abzuschneiden“. Wir setzen dazu alle | z| > 2 (ein übliches Ausreißerkriterium) je nach Vorzeichen auf den Wert +1 oder –1. Abbildung 4 zeigt, wie sich unterschiedliche Maßnahmen auf die Verteilung der Merkmalswerte auswirken. Die Vektor-Normalisierung (links unten) führt nur zu minimalen Änderungen und reduziert die Anzahl von Ausreißern praktisch nicht. Abschneiden großer z-Werte wirkt sich nur auf überdurchschnittlich häufige Wörter aus (rechts oben). Wie in Abbildung 5 zu sehen ist, wird durch diese Maßnahme ebenfalls die Qualität aller L p-Deltamaße deutlich verbessert. Der positive Effekt fällt aber merklich geringer aus als bei der Vektor-Normalisierung.
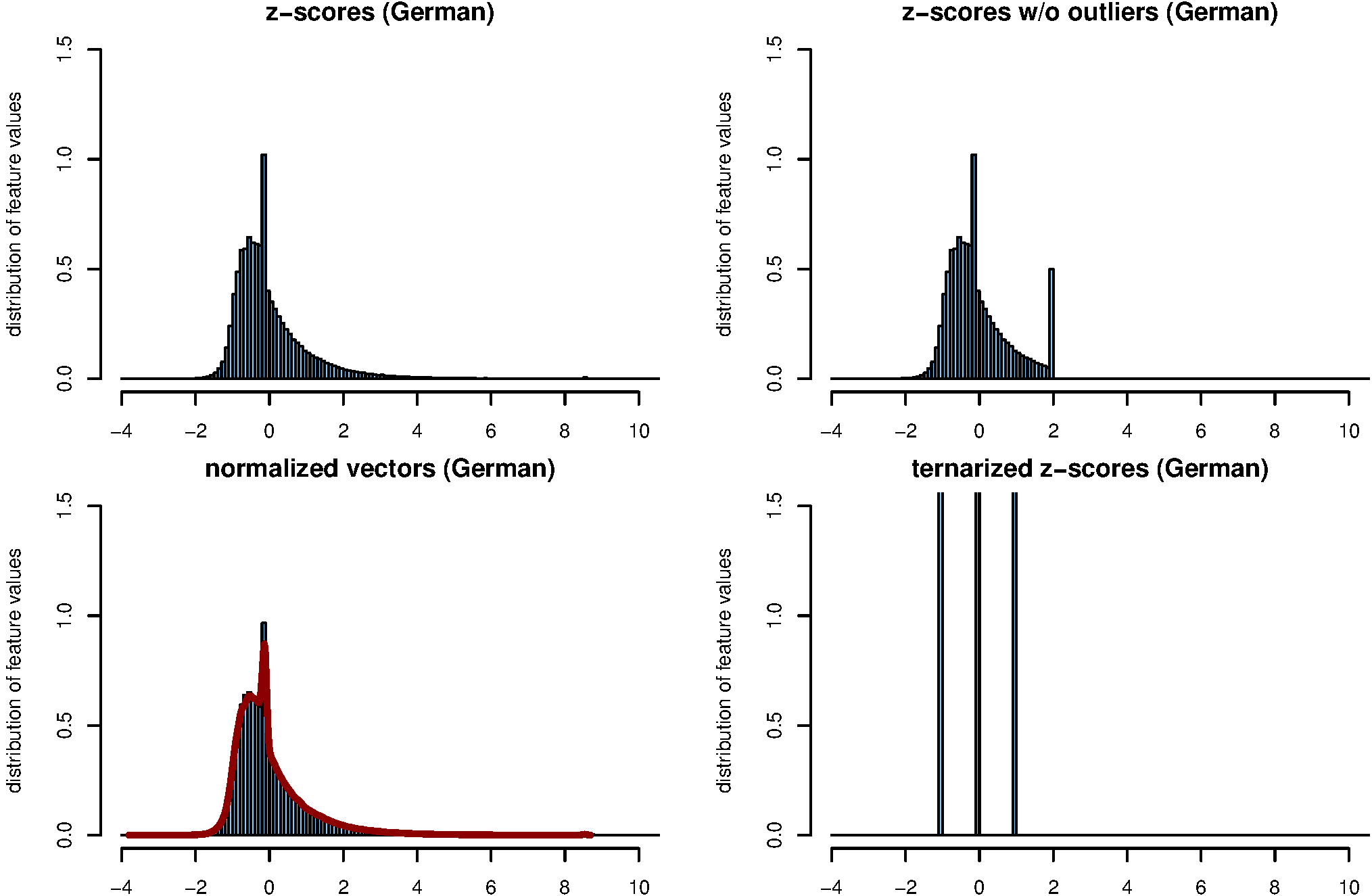
Abb. 4: Verteilung von Merkmalswerten über alle 75 Texte bei Vektoren mit 5000 MFW. Gezeigt wird die Verteilung der ursprünglichen z-Werte (links oben), die Verteilung nach einer Längen-Normalisierung (links unten), die Verteilung beim Abschneiden von Ausreißern mit | z| > 2 (rechts oben) sowie eine ternäre Quantisierung in Werte –1, 0 und +1 (rechts unten). Im linken unteren Bild gibt die rote Kurve die Verteilung der z-Werte ohne Vektor-Normalisierung wieder; im direkten Vergleich ist deutlich zu erkennen, dass die Normalisierung nur einen minimalen Einfluß hat und Ausreißer kaum reduziert. Grenzwerte für die ternäre Quantisierung sind z < –0.43 (–1), –0.43 ≤ z ≤ 0.43 (0) und z > 0.43 (+1). Diese Grenzwerte sind so gewählt, dass bei einer idealen Normalverteilung jeweils ein Drittel aller Merkmalswerte in die Klassen –1, 0 und +1 eingeteilt würde.
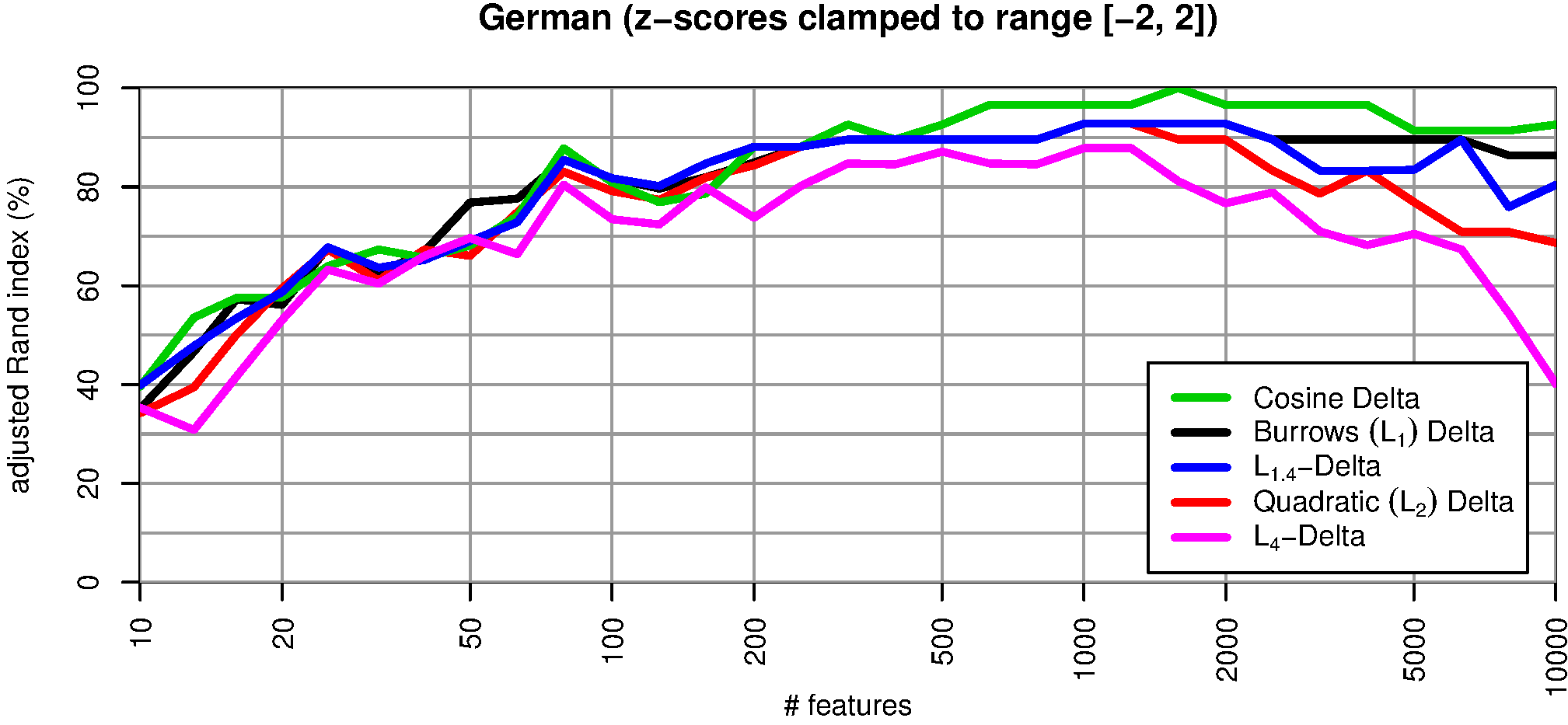
Abb. 5: Clustering-Qualität nach „Abschneiden“ von Ausreißern, bei dem Merkmalswerte | z| > 2 je nach Vorzeichen durch die festen Werte –2 bzw. +2 ersetzt wurden.
Insgesamt erweist sich Hypothese H1 somit als nicht haltbar. H2 wird durch das gute Ergebnis der Vektor-Normalisierung unterstützt, kann aber nicht unmittelbar erklären, warum auch das Abschneiden von Ausreißern zu einer deutlichen Verbesserung führt. Um diese Hypothese weiter zu untersuchen, wurden reine „Schlüsselprofil“-Vektoren erstellt, die nur noch zwischen überdurchschnittlicher (+1), unauffälliger (0) und unterdurchschnittlicher (–1) Häufigkeit der Wörter unterscheiden (vgl. Abb. 4, rechts unten).
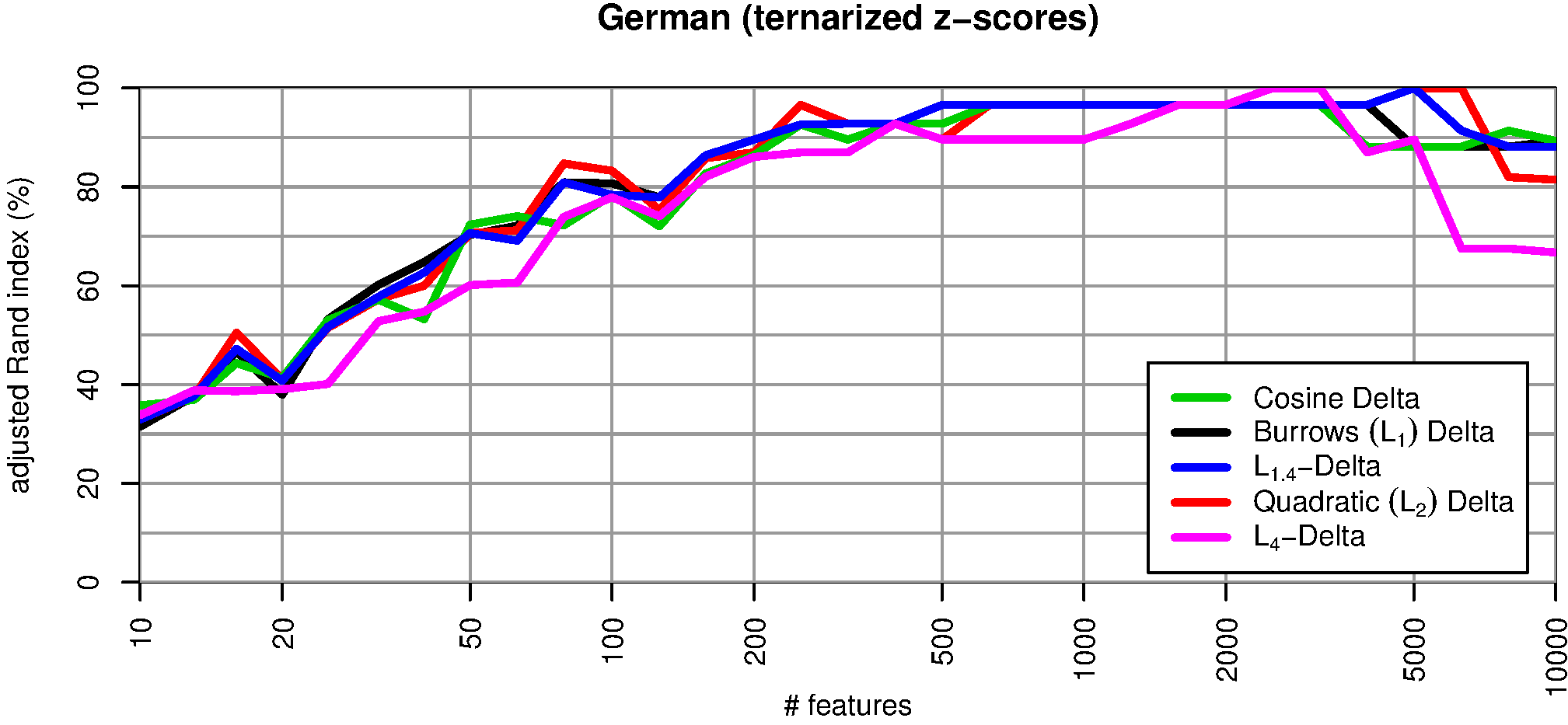
Abb. 6: Clustering-Qualität bei ternärer Quantisierung der Vektoren in überdurchschnittliche (+1, bei z > 0.43), unauffällige (0, bei –0.43 < z < 0.43) und unterdurchschnittliche (–1, bei z < –0.43) Häufigkeit der Wörter.
Abbildung 6 zeigt, dass solche Profil-Vektoren hervorragende Ergebnisse erzielen, die der Vektor-Normalisierung praktisch ebenbürtig sind. Selbst das besonders anfällige L 4-Deltamaß erzielt eine weitgehend robuste Clustering-Qualität von über 90%. Wir interpretieren diese Beobachtung als eine deutliche Bestätigung der Hypothese H2.
2.3. Diskussion und Ausblick
H1, die Ausreißerhypothese, konnte widerlegt werden, da die Vektor-Normalisierung die Anzahl von Extremwerten kaum verringert und dennoch die Qualität aller L p-Maße deutlich verbessert wird. H2, die Schlüsselprofil-Hypothese, konnte dagegen bestätigt werden. Die ternäre Quantisierung der Vektoren zeigt deutlich, dass nicht das Maß der Abweichung bzw. die Größe der Amplitude wichtig ist, sondern das Profil der Abweichung über die MFW hinweg. Auffällig ist das unterschiedliche Verhalten der Maße, wenn mehr als 2000 MFW verwendet werden. Fast alle Varianten zeigen bei sehr vielen Features eine Verschlechterung, aber sie unterscheiden sich darin, wann dieser Verfall einsetzt. Wir vermuten, dass das Vokabular in diesem Bereich weniger spezifisch für den Autor, und eher für Themen und Inhalte ist. Die Klärung dieser Fragen wird zusätzliche Experimente erfordern.